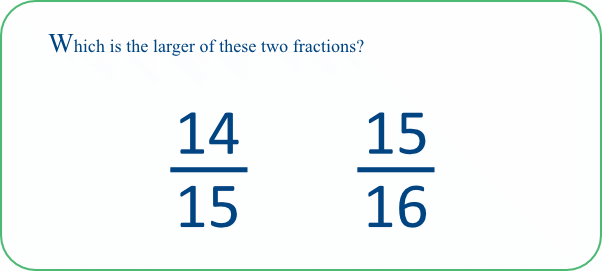FRA01: Comparing two fractions

We start with two unusual, random-looking fractions, which pupils are asked to compare. You might feel that this is plunging pupils in too deep, in which case you could start with another of this Week's tasks, which involve more familiar fractions. On the other hand, the task might reveal something interesting about pupils' thinking, once they have got over the 'shock'. What is there to loose?!

[Note: In the third week's tasks, we look at placing fractions on a number line. You might find it helpful to ask pupils to place the fractions in this week's task on a number line too.]

TASK 01A: It is likely that these fractions will seem quite unusual to many pupils, and some might feel overwhelmed by them. On the other hand, pupils might well enjoy the challenge, especially with a bit of encouragement: given time to think, pupils might come up with some revealing attempts at making sense.

In a class of pupils, several strategies for comparing the fractions are likely to emerge, some valid and some not; we take a closer look at some of these in later Weeks.

Younger pupils might well decide that 99/204 is the larger fraction because the individual numbers are larger than in the other fraction. This is often seen as a sign of natural (or whole) number bias. Others might opt for 17/19 because 17 is only 2 away from 19, whereas 99 is much further from 204. This is an example of gap thinking, which works here but is not generally valid (since it is additive rather than multiplicative) - you might want to ask pupils for an example where it does not work!

Some pupils might correctly choose 17/19 because it is much closer than 99/204 to 1 (an example of residual thinking). Others might make use of 1/2 as a benchmark: 99/204 is slightly less that a half, 17/19 is a lot more. Older (?) pupils might compare the (scalar) relationship between the numerators with the (scalar) relationship between the denominators: 204 is about 10 times 19, but 99 is a lot less than 10 times 17. Similarly, they might compare the (functional) relationship or ratio between numerator and denominator: 204 is roughly twice 99, whereas 19 is far less than twice 17.

In class, you might want to challenge pupils to come up with other 'unusual' fractions to compare, perhaps with a focus on 'easy' or on 'difficult' pairs. Or you might ask for four 'random' numbers and then use these to form various pairs of fractions for pupils to compare.

TASK 01B: This turned out to be the easiest of the 8 items used by Clarke and Roche. In their sample of 323 Grade 6 pupils (11 - 12 year olds), 77% chose the correct fraction (7/8) and gave a valid reason. Of course, this still leaves almost a quarter of their sample who were not deemed successful, perhaps because their explanation involved natural number bias ('7/8 is larger because the numbers are larger').

For many pupils, the task will seem trivial, and you might even decide not to use it. Its main interest perhaps lies in the fact that a 'parallel' item used by Clarke and Roche, in which the numerators were the same, rather than the denominators, proved to be far more challenging. That item is shown next.

TASK 01C: In this item, the correct fraction (along with a valid reason) was chosen by only 37% of Clarke and Roche's sample, compared to 77% for their item with the same denominator (Task 01B, above). This is a remarkable difference, and is probably due in large part to the fact that pupils are taught to 'make the denominators the same' when comparing fractions. As such, the task is a nice vehicle for encouraging pupils to think more flexibly.

It would be interesting to see how performance on this and the previous task compares for younger pupils, that is, pupils who have not yet been taught to make the denominators the same. Would their performance on the two items be similar? And what would happen if we used more 'difficult' denominators, as in the variant below? Would that prompt more pupils to look for an alternative strategy?

Another variant that could promote this more flexible thinking is shown below, where one numerator is a simple multiple of the other. [Both fractions are close to one quarter, so the task might also attract benchmark thinking - something we look at more closely in next Week's tasks.]

TASK 01D: This is another fascinating item from Clarke and Roche, in that it was answered correctly by only 15% of their sample. A seemingly neat way to solve this is to use residual thinking, based on the observation that the fractions are just 1/6 and 1/8 away from 1. To interpret this correctly, one has to use the fact that the larger denominator (in this case 8) indicates the smaller residue; in turn, this smaller residue indicates that 7/8 is the larger of the original fractions. We have found that pupils often stumble at this last step and wrongly conclude that 7/8 is the smaller - a 'nice' example of cognitive overload!

Another interesting feature of the item is that some pupils will conclude that the fractions are equal, because the gap between numerator and denominator is 1 for both. Put another way, we've 'done the same' to the numerator and denominator of 5/6 by adding 2 to both! This kind of additive thinking is difficult to fully overcome (even if we use residual thinking to show that it is wrong). How do we shift pupils' thinking towards a multiplicative view such as this?

Adding 2 to the numerator 5 has a greater relative impact than adding 2 to the larger denominator 6, so this produces a larger fraction.

It might be interesting to give pupils a variant such as the one below, where the fractions are closer together. Will more or the same number or fewer pupils think they are equal?

TASK 01E: This proved to be the most challenging of the items used by Clarke and Roche, with a facility of only 11%. It is amenable to residual thinking but pupils might need to take an extra step to compare the residues 2/9 and 1/4 - for example by transforming 1/4 into 2/8.

Another approach would be to convert 3/4 into 6/8, but pupils doing this might still succumb to additive thinking: 'adding 1 to 6 and to 8 changes 6/8 into 7/9, so the fractions are equal'.

Here an efficient approach, though perhaps not as neat as using residues, is to use the notion of common denominators to convert the fractions to 28/36 and 27/36. Similarly (?), some pupils might convert the fractions to the decimals 0.7 recurring and 0.75.

Of course, we could also transform the fractions so that they have common numerators, for example 21/27 and 21/28. It would be interesting to see whether any pupils think of doing that!