Here we think of fractions in the context of fair shares. This carries two meanings, that of fraction as quotient and fraction as parts of a whole. For example, if we share 3 (identical) cakes fairly among 4 people, then we divide the 3 cakes into 4 equal pieces, with each person ending up with 3 out of 4 equal parts of a cake.
Task 12A: Mathematically, the simplest way of sharing the three pizzas is to cut each into 4 identical pieces. Each person gets 3. However, in practice, the pizzas can be shared more simply, with fewer cuts.
We can think of Method 4 as representing the situation where the pizzas arrive, and are shared, one at a time. [Leen Streefland calls this 'French division'.] Does this result in the same total share as when the pizzas all arrive together (as in Method 1, say)?
Note: When we describe each person's share, it is worth being clear about the unit that we are measuring in. Is our unit (or 'whole') one pizza or all the pizzas? In Method 4, we have 12 equal pieces, with each person receiving 3. This might lead some pupils to say that each person's share is 3/12, or 1/4. This is true in the sense that each person gets 1/4 of all the pizzas. Of course, this is equivalent to 3/4 of one pizza.
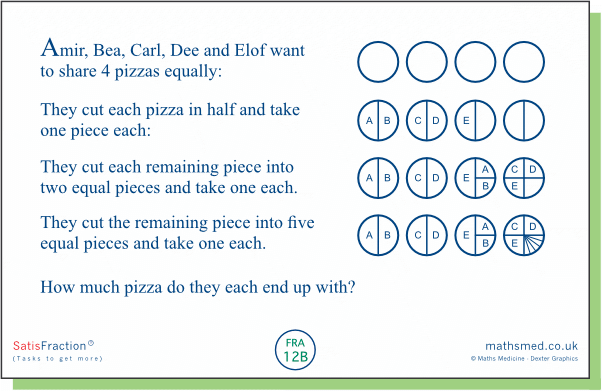
Task 12B: Here each person is give 1/2 + 1/4 + 1/20 of a pizza. It is fairly easy to see that this is '3/4 and a bit'. But how obvious is it to pupils that sum must be 4/5? The calculation should provide a nice challenge for some pupils.
[1/2 + 1/4 + 1/20 = 10/20 + 5/20 + 1/20 = 16/20 = 4/5.]
Some pupils might adopt an informal, grounded approach like this to evaluate an individual share:
a share consists of '3/4 plus a bit' of a pizza; this is the same as 5+5+5+1 'bits'; this is the same as 4 out of 5 equal parts.
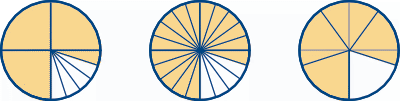
Task 12C: Here we have the same scenario as in Task 12B, but the pizzas are cut up differently. Also a small piece of Pizza gets lost, so each person's share will be slightly less than 4/5 of a pizza - how much less?
Each person's share can be written as 2/3 + 1/9 of a pizza. Can pupils evaluate this?
[2/3 + 1/9 = 6/9 + 1/9 = 7/9.]
And can pupils see that 7/9 is close to (and less than) 4/5 (or 8/10)? And can they determine how much less?
[4/5 – 7/9 = 36/45 – 35/45 = 1/45.]
You might want to ask pupils to think of other ways of cutting up and sharing the pizzas. It can be a nice challenge and provides plenty of scope (and an actual rationale!) for manipulating fractions.
Task 12D: Here we have the same numbers as in task 12A so pupils can use similar methods to determine that the desired fraction is 3/4 (of a bar) for each of the 4 friends. This time the objects being shared (chocolate bars rather than pizzas) can each be broken into 48 pre-determined pieces, so it is fairly easy to form 3/4 of a bar - it consists of 36 pieces.
The task becomes more challenging with the arrival of Gerald. It is no longer possible to share the bars equally using only whole pieces.
The number of pieces, 36, that each of the four friends gets initially, can be found in different ways. Some pupils might find a way of calculating 3/4 of 48. Others might count or calculate the number of pieces inside the various parts into which they have partitioned the bars. Others might calculate the total number of pieces (3×48) and divide this by 4.
A systematic way of determining the number of pieces that the friends should give to Gerald is to make a list of ordered pairs such as this, below. (The first number represents the number of pieces that each of the 4 friends has kept; the second number is the total number of pieces that Gerald has been given.)
(36, 0), (35, 4), (34, 8), (33, 12), (32, 16), (31, 20), (30, 24), (29, 28), (28, 32), ....
(29, 28) is the fairest solution if we are keeping to whole pieces.
[Check: 4×29+28 = 116+28 = 144 = 4x48.]
Some pupils might see a way of curtailing this approach. The four friends plus Gerald should end up with about 3/5 of a bar each. 3/5 of 48 is a bit less than 3/5 of 50 = 30.
There are other ways we can play with the fractions, such as this:
the four friends reduce their share from 3/4 to about 3/5;
3/4 – 3/5 = 3/20, and 3/20 of 48 pieces is about 7 pieces.
36 – 7 = 29.
Task 12E: This is similar to Task 12D, but this time the task resolves itself nicely. Initially, the four friends receive 3/4 of a bar, which is 3/4 of 40 pieces, which is 30 pieces. When Geraldine comes along, if the four friends all give her 6 pieces, they all end up with 24 pieces. And 24 = 3/5 of 40.