FRA09: Finding a third

In this family of tasks we are given the position of one fraction on a number line and are asked to locate the position of the fraction ⅓. It is easy to vary the task, to make it more or less challenging.

TASK 09A: We start with the simplest of all fractions, ½, for the given fraction. The task, though, could pose quite a challenge to some pupils.

A neat way to solve the task is to convert the two fractions to fractions with the same (common) denominator, in this case sixths: ⅓ is 2 sixths and ½ is 3 sixths, so ⅓ is two-thirds of the way along the interval from 0 to ½.

Some pupils might work in a more intuitive way by making use of the fact that ½ lies midway between ⅓ and ⅔. This might lead to markings like those on the first number line below, which can then be adjusted to make the intervals from 0 to ⅓ and ⅓ to ⅔ look to be the same length, as in the second line below.  Then, having produced a drawing that 'looks' about right, pupils could be asked to compare the sizes of the intervals between 1/3 and 1/2, and 0 and 1/3.

TASK 09B: The first task was quite challenging. This will be more challenging for many pupils, but perhaps not for those familiar with the notion of common denominator: the fractions can both be converted to 12ths. Pupils who were given Task 09A might also spot that we can transform this task into Task 09A by using the position of ¼ to locate the position of ½.

A simple way to vary the task is to replace ¼ with other unit fractions such as ⅕ or ⅟₇. This doesn't alter the nature of the task substantially, other than that the fractions might be less familiar to pupils and the fact that the practicalities of locating ⅓ are made more challenging by having to make use of smaller intervals. [Also the desired fraction ⅓ might be off the page....].

Here are two more variants, both simpler than the original task.
 

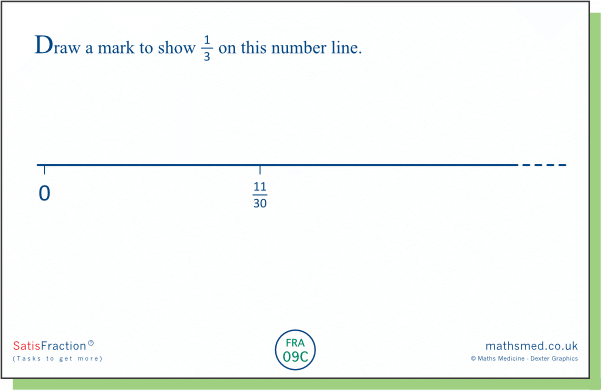
TASK 09C: Here is a variant where we might be content with a qualitative answer: ⅓ is a 'tiny bit' to the left of the given fraction. 

Regardless of the accuracy of pupils' marks for the location of 1/3 on the number line, you might want to discuss the true size of the 'tiny bit' between 1/3 and 11/30. For this, the diagram below could be useful at some stage.
 

We could make the task still more challenging by choosing a fraction whose denominator, unlike 30, is not a multiple of three, for example 10/31. The desired fraction 1/3 will lie slightly to the right of this fraction, but how far to the right? This can be solved by converting the two fractions to 31/93 and 30/93. Some pupils might adopt a slightly more grounded approach, by thinking of 1/3 as 10⅓/31 which of course is equivalent to 31/93.

Task 09D: In this variant we are given the fraction 1/3 on the number line and are asked to locate a second fraction. The fractions here match those in Task 09B.

We could scaffold the task by splitting the interval from 0 to 1/3 into suitably smaller equal parts, as here:

Or what about this?!

TASK 09E: In this variant the fractions have a similar structure to those in Task 09C: the given fractions are quite close together and one of the denominators (21) is a multiple of the other (3). We might again be content with a qualitative answer: 8/21 is a 'tiny bit' to the right of the given fraction.  

Some pupils might be able to determine that the gap between 1/3 and 8/21 is 1/21, which can be derived from the diagram below.