This week's set of tasks offers a continuation of last weeks's, but is probably more accessible. The individual fractions are simpler, but are repeated several times.
Task 17A: Here we make use of the classic 'diamond' method of halving the area of a square - by rotating a given square through 45˚ and shrinking it until it fits tightly inside the original square. The orange region is formed by halving the blue outer square and then halving and halving again. So its area is one eighth of the original square. The lemon region is formed by taking one third of the blue outer square, then taking a third of the resulting strip. So its area is one ninth of the original square.
Task 17B: Here we mix the operations. The area of the orange region is ½×½×⅓×⅓ of its blue outer square. The area of the lemon region is ⅓×⅓×½×½ of its blue outer square. So they are both ¹⁄₃₆ of the blue outer square.
Task 17C: We can express the fractions as, say, ⅕ × ⅕ × ½ and ⅟₇ × ⅟₇ respectively. So the lemon region is slightly larger.
Task 17D: This time the fractions are the same. We have ⅕ × ⅕ × ¼, say, and ⅟₁₀ × ⅟₁₀, say. So they are both ⅟₁₀₀.
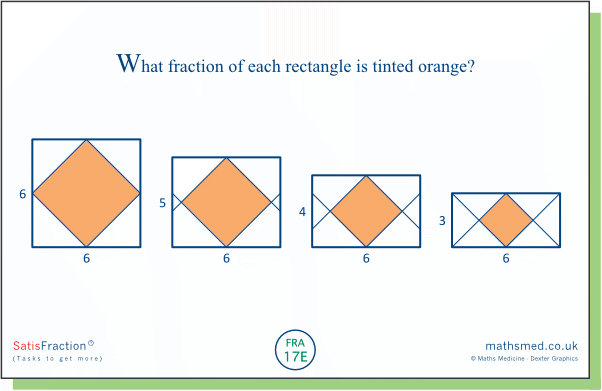
Task 17E: We finish with something more challenging. We can see that the diagonals of the orange squares are 6 units, 5 units, 4 units and 3 units long, respectively. So their areas are half of 6², 5², 4² and 3² square units, respectively. This means that they cover 6/12, 5/12, 4/12 and 3/12 of their respective rectangles (or 1/2, 5/12, 1/3 and 1/4 - though this obscures the pattern in the set of fractions).
the area of the 'diamond' is ½h²
and so the fraction is ½h²/6h = h/12.
