Here we look at ways of performing the division ¾ ÷ ²⁄₉. We adopt two approaches. One is to interpret and to visualise the division as quotition. The other is to transform fractions in ways that produce expressions that are easier to evaluate.
Task 18A: The number line is not essential for the items in this task and some pupils will probably ignore it. However the line can serve as a safety net (?!) for checking whether an answer makes sense.
The first item is straightforward.
In the second item, some pupils might be tempted into writing 2/3; however, this gives us a larger fraction than we started with, which doesn't make sense.
Some pupils might baulk at the third item, others might use a formal procedure or argue that the answer must be the reciprocal of the answer to the first item; of particular interest here is whether pupils can come up with a sensible estimate, perhaps based on a quotitive view of division (How many two-nineths are there in 2?) or a partitive view (If 2/9 of a share is 2, what is one share?).
The fourth item is similar to the third, though pupils who solve it might be puzzled by how we get an answer, 13½, that involves the fraction ½. Where did the half come from? Half of what?!
Task 18B: This is nudging pupils towards the idea of division as quotition:
"How many times does 2/9 go into 3/4?", or
"How many times does the brown line fit into the yellow line?".
To keep things focussed, the emphasis is on estimation rather than on finding the exact answer, though pupils might well go on to attempt that. We can see that the brown line fits more than 3 times but less than 4 times into the yellow line (or indeed more than 3¼ times and less than 3½ times). Note that we haven't numbered the scales on the number line, but that our unit, when it comes to the division, is the length of the brown line.
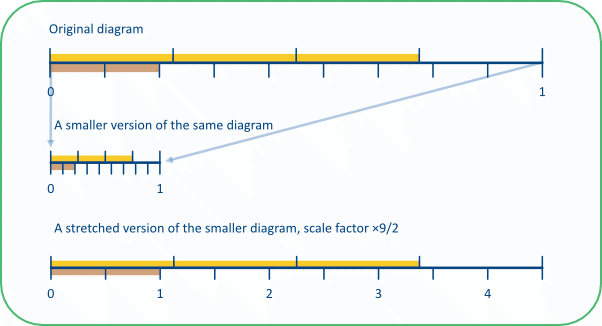
Digression: The task can be approached in other ways, of course. For example, one could imagine stretching the diagram containing the brown and yellow lines until the brown line is 1 unit long (below), using the scale factor ×⁹⁄₂. The yellow line would then be a little under 3½ units long (actually ¾ × ⁹⁄₂ = 3⅜). In effect, what we are doing here is changing both terms of the expression into something more convenient, by multiplying or dividing both fractions by the same number, on the principle that a/b = na/nb. We pursue this further in Task 18E.
We can also model the above stretch, with its scale factor of ×⁹⁄₂, using a double number line (DNL) such as the one below.
We could also set up a table like this and explore it on the basis that the relationship between the numbers in the columns (and rows) is multiplicative.
Task 18C: Here we work our way, step by step, to the division expression that we are ultimately interested in (¾ ÷ ²⁄₉). We start with a much simpler expression that it is hoped pupils can visualise, and then transform the division in further simple steps. Though these steps are simple in themselves, the situation might well become more abstract for pupils - how well do they cope?
The value of the expression in the first line is 9. (Why?) In the second step we halve that (4½). We then divide by 4 (1⅛). Finally we multiply by 3 (3⅜).
Task 18D: Again, we start with a (very) simple expression and move to our goal in simple steps.
The result of step 1 leaves ¾ unchanged. In step 2 we divide by something 9 times as small so the result will be 9 times as large (27/4 or 6¾). In step 3 we halve the current result (3⅜).
You might want to check whether pupils have understood the methods demonstrated in this and the previous task, by asking them to replicate the methods with a division similar to ¾ ÷ ²⁄₉.
Task 18E: Here we start with the desired division expression and transform it into equivalent expressions by multiplying or dividing both fractions in the expression by the same number. Identifying these transformations is quite challenging.