In this Week's tasks we use a number line, in particular the segment from 0 to 1, to represent fractions. The line provides an important model that can help pupils develop the notion of fraction as a measure or number. Also, by representing the magnitude of a fraction as a length, pupils might develop a sense of how this magnitude expresses the ratio relation between the two numbers (numerator and denominator) that form the fraction.
The number line can also bring out a key difference between natural numbers and fractional (or rational) numbers: whereas any given natural number has a unique successor, there is no unique 'next' fraction - for any pair of fractions we can always find a fraction that lies between them. We explore this in later Weeks.
[Note: There is a subtle difference between the two versions of the 0 to 1 line segment shown below. The first version indicates that the line continues and could be used to represent our familiar counting numbers 1, 2, 3, etc and that our fractions are part of this family of numbers. The second is rather like a finite bar, and so will tend to evoke the more narrow notion of fraction as parts of a whole. We use the first version in the tasks below, though the distinction may be too fine to make explicit for most pupils at this stage.]
TASK 03A: Here pupils are asked to estimate the position of a fraction. It is likely that pupils will interpret this in different ways - some quite loosely, perhaps involving a quick estimate by eye, some more tightly, perhaps involving partitioning or measurement. The primary purpose of the task is to ascertain the variety of methods that pupils use so that they can be discussed and shared.
Some pupils might spot and be content to use the fact that the fraction is somewhat less than a half. Others might notice that it is close to one third, in fact slightly more. Or they might argue that it lies between a quarter (5/20) and a half (10/20) and slightly nearer the former (in other words, slightly less than 7½/20 = 3/8!). Others might try to visualise where 7 goes on a line from 0 to 20. Or pupils might try to partition the line into smaller, equal parts. This can be done in various ways - do pupils partition the whole line, or perhaps just the first half, in which case do they partition this into, say, 5 parts, or two lots of 5, or do they attempt 10 parts in one go?
To discuss such ideas further you could use this variant of the task. Ideally, the lines should be revealed one at a time.
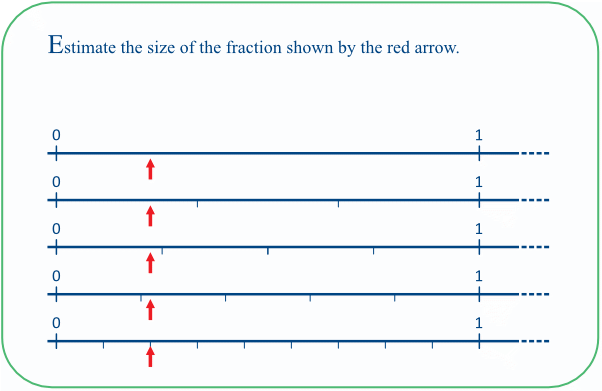
TASK 03B: In contrast to the previous task, this time we are given the position of the fraction and are asked to estimate its value. It is likely that most pupils will come up with the unit fraction 1/4, 1/3 or 1/5 as their first estimate. All these could be regarded as 'quite good', given that the actual fraction is 2/9. In fact this lies between 1/4 and 1/5, and is slightly closer to 1/5.
This variant provides a nice, informal setting for thinking about equivalent fractions and fractions of fractions. For example, the second line might prompt pupils to partition the first 1/3 interval into 3 equal parts, each of which would therefore be 9ths, with the arrow pointing at about 2/9 (in fact, exactly 2/9!).
The 3rd line might suggest to pupils that the arrow is pointing at roughly 9/10 of 1/4, or 9/40.
The 4th line might result in an estimate such as 1/5 + 1/10 of 1/5 = 10/50 + 1/50 = 11/50.
The 5th line reveals the actual value, 2/9.
A further challenge would be to get pupils to compare the resulting fractions. A quick and efficient way, and one which highlights the notion of fraction as a quotient, would be to use a calculator to convert the fractions to decimals: 2/9 = 0.2 recurring, 9/40 = 0.225, 11/50 = 0.22
TASK 03C: Here we work just with a whole number on the number line. This might seem like a backward step, but it leads to a nice way of thinking about the position of fractions on the number line. We pursue this in the next task.
As with earlier tasks, pupils might approach this in a variety of ways. Here are some things to look for or perhaps to develop:
On the 0 to 9 number-line segment, 5 lies slightly more than half way along the segment;
On the 0 to 8 segment, 5 will now be slightly further to the right;
On the 0 to 16 segment, 5 will be slightly less than one third of the way along the line from 0; it will also be half as far from 0 as on the previous segment.
On the 0 to 49 segment, 5 will be just over one tenth of the way along, and about one third as far from 0 as on the previous segment.
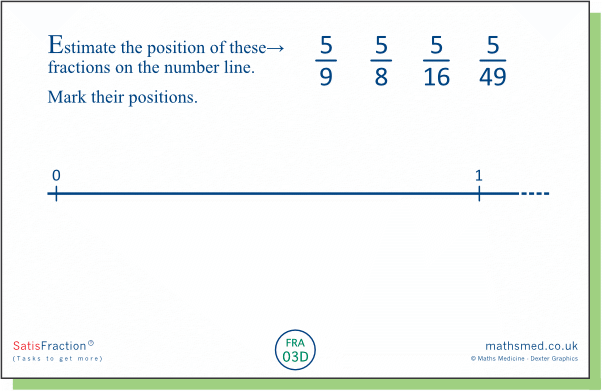
TASK 03D: We can find the position of a fraction on the number line, by temporarily replacing the number 1 with the fraction's denominator and thinking of the position of the numerator on the resulting segment. This temporarily transforms the task into the previous one (Task 03C), and we should end up with the same relative positions on the segment.
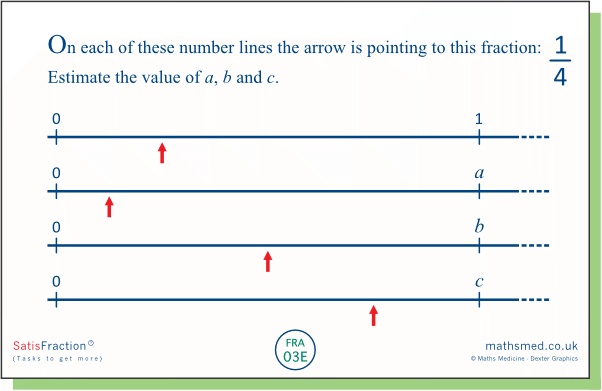
TASK 03E: The Red Arrows, in some kind of formation!
This is a relatively simple task (except for the last part perhaps). It is designed to highlight the idea that the number line is continuous, even though we focus only on part of it.